网站首页 文章专栏 接雨水 & 最大点
问题一: 盛最多水的容器
leetcode题号:11
题目
给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
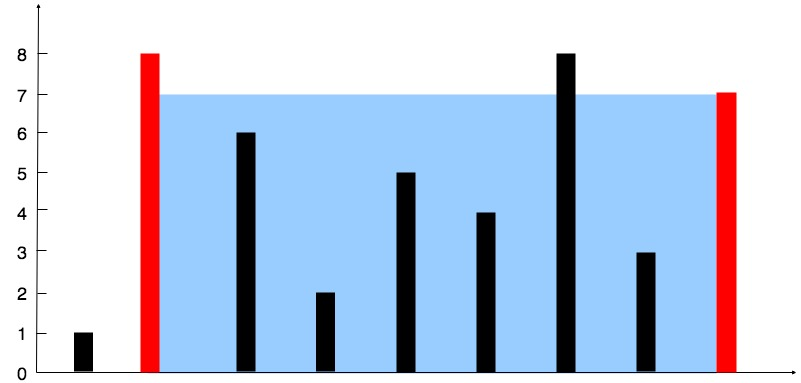
示例:
输入:[1,8,6,2,5,4,8,3,7] 输出:49
解答
左右两个指针,比较矮的一堵墙向中间走,一直走到两个指针相遇。
最基础的解法当然是选择两个当容器,复杂度为O(n^2), 这种解法显著降低了复杂度。为什么非要是较低的指针向中间走呢?难道不害怕错过解空间?
实际上,area = min(height[l], height[r]) * (r - l), 较大值向中间走后,(r - l)是一定减小的,设走之后遇到的值为height[m](这里假设l与r不动), 如果height[m] > min(height[l], height[r]),计算面积时还是采用min(height[l], height[r]),并不会增加。所以面积是一定减小的。
所以该问题可以归类为解空间的优化,从O(n^2)降为O(n), 依赖观察与计算。
class Solution { public: int maxArea(vector<int>& height) { int res = 0; for(int i = 0, j = height.size() - 1; i < j;){ res = max(res, (j - i) * min(height[i], height[j])); height[i] < height[j] ? i++ : j--; } return res; } };
问题二:接雨水
leetcode题号:42
题目
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。 感谢 Marcos 贡献此图。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1] 输出: 6
解答
虽说有人将这种方法称为双向dp,但我觉得不妥。归结为记录扫描过程中的最大值最好。
仔细观察题目中的图片,一定会有最高值,然后雨水在中间的凹陷处。那么我们从左侧开始扫描,只记录最大值;从右侧开始扫描,同样只记录最大值。然后取两个最大值中的较小者作为dp值。这时候dp值减去当前值就是所接的雨水。

class Solution { public: int trap(vector<int>& height) { if(height.size() == 0) return 0; vector<int> dp(height.size()); int left_max = height[0]; int right_max = height[height.size() - 1]; for(int i = 0; i < dp.size(); i++){ left_max = max(left_max, height[i]); dp[i] = left_max; } for(int i = (int)dp.size() - 1; i >= 0; i--){ right_max = max(right_max, height[i]); dp[i] = min(right_max, dp[i]); } int res = 0; for(int i = 0; i < dp.size(); i++){ res += dp[i] - height[i]; } return res; } };
问题三:二维点集中的最大点
题目
P为给定的二维平面整数点集。定义 P 中某点x,如果x满足 P 中任意点都不在 x 的右上方区域内(横纵坐标都大于x),则称其为“最大的”。求出所有“最大的”点的集合。(所有点的横坐标和纵坐标都不重复, 坐标轴范围在[0, 1e9) 内)
如下图:实心点为满足条件的点的集合。请实现代码找到集合 P 中的所有 ”最大“ 点的集合并输出。
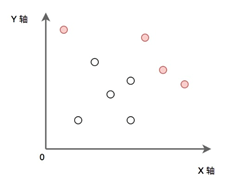
解答
对于所有的点先按照y从大到小排序O(NlongN) 从大到小遍历排好序的点集,当前y是出现过的最大的y,即是需要的结果,进行输出O(N)。 总体时间复杂度为O(NlogN)
还可以这样理解,从y轴向下走,记录x值的最大值。如果有点打破了x值记录,就纳入最大点的结合。还是一种边走边记录最大值的方法。
#include<iostream> #include<vector> #include<algorithm> using namespace std; int main() { ios::sync_with_stdio(false);//提升cin和cout的性能 int n_pointer=0; cin>>n_pointer; vector<pair<int,int>> xys; for(int i=0;i<n_pointer;i++) { int x,y; cin>>x>>y; xys.push_back(make_pair(x,y)); } sort(xys.begin(),xys.end(),[](pair<int,int> &p1,pair<int,int> &p2)->bool{ return p1.second>p2.second; }); int max_x=-1; for(auto &pair:xys) { if(pair.first>max_x) { cout<<pair.first<<" "<<pair.second<<endl; max_x=pair.first; } } return 0; }
对比分析
问题二与问题三都是边走边记录最大值的方法,适合于和图形相关的包裹、边界问题。
问题一与问题二外观相似,但是核心不同。问题二的纵坐标是有宽度的,会影响蓄水。
后续还有接雨水2,以及其他的相似题目待解答分析。